Making a piston move correctly can be tricky, but here is a way to do it. I'm using expressions to solve it, because this makes it a bit easier and manageable.
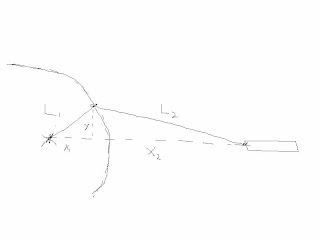
First of all, consider this picture:
The distance between the center of the wheel is the sum of x1 and x2. Finding x1 is simple trigonometry (x1 = cos(rotation of the wheel)*L1).
Finding x2 is a bit trickier. Not much though.
Y, L2 and X2 also forms a triangle. We can set L2 to whatever length we want it to. Y varies with the rotation, and can be found with sin(rotation of the wheel)*L1.
So, we know have L2 and Y, and using Pythagoras theorem, we can calculate x2.
The code can look something like this:
float $l2 = 10; // Decide on L2
float $y = LOC_Radius.translateY*sind(LOC_Center.rotateX+90); //Calculate Y
float $x1 = LOC_Radius.translateY*cosd(LOC_Center.rotateX-90); //Calculate x1
float $x2 = sqrt($l2*$l2-$y*$y); //Calculate x2 from y and L2
LOC_Piston.translateZ = $x1+$x2; //Add x1 and x2 together to get the total translation.
LOC_Radius - where the first cylinder connects to the wheel
LOC_Center - Center of the wheel
LOC_Piston - the "pushing point" of the piston
After that, I just added some geometry to the locators so that it looks like a wheel and a piston. Mostly done with some parenting, point constraings and one aim constraint.
The result can be seen here:
